これは、よろこばしいこと。
英語だけでなく、統計もできるようになりたい。
Toshi
(2023/5/9追記)
・多変量解析やれば交絡因子を補正できる。
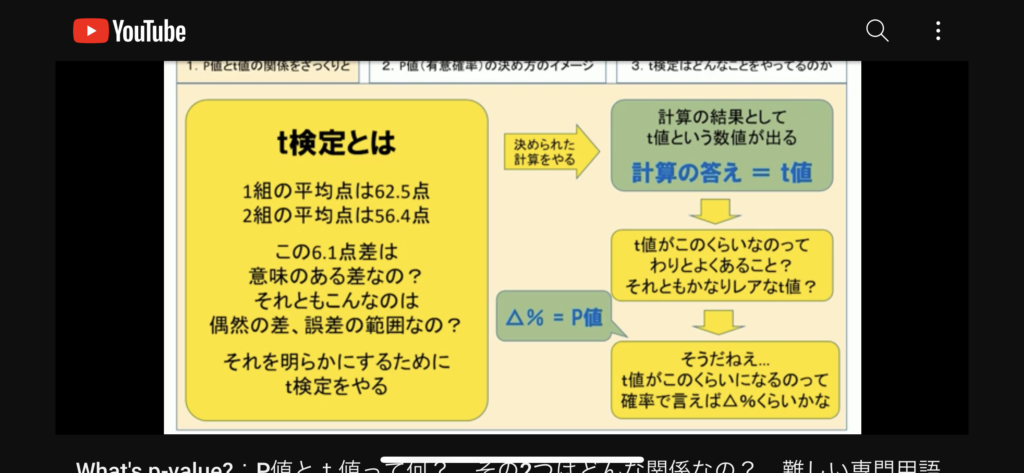
・傾きの比(の対数をとったハザード比)を定式化できる。その変数が妥当かどうかはt検定してみればわかる。解析して、検定する、の流れ。
・t 検定は二群の平均の差を検定する。Χ二乗検定は二群の割合の差を検定する。

・proportional hazardは成り立たない?
・傾向スコアマッチング法は、二群の条件を合わせるために補正を行うもの。
・正規分布に従わないものの検定もできる。
・何回も検定すると多重性という問題が発生する。(たくさん検定すれば一回ぐらい有意差でるっしょ!みたいな)
・(単変量or多変量)Cox比例ハザード分析
Cox…統計学者の名前
比例…線形。直線で近似するということ。
ハザード…ハザード比は一定という仮定に基づいてる
分析…モデル。式を作るってこと。
→作った式が有効か?は、検定して確認すること!!
・リスク比とハザード比は違う。
リスク比はリスク何倍とか言えるけど、ハザード比は言えない。オッズ比も然り。
どういう時にオッズが出てくるんだっけ?
・結局、何かが独立した予後因子だとわかるためには、これとこれとこれとこれでモデル式が立てられるよということを示して、
その独立変数全てが検定を通過する、ことが必要。
独立変数は複数ある、というかセットなの。
セットだから価値がある。ここ頭の転換が必要。
これはそう、これは違う、ではなくて、「どういうモデル(独立変数と、係数(偏回帰係数)の組み合わせ)」を構築するかなの!
・ロジスティック回帰分析:この二つが本質。結果の変数が2つしかない場合。(合格と不合格とか)


説明できるモデル式を作って、その説明結果が妥当であるか検定で確かめるというのはどの分析でも同じ。
(2024/10/15追記)
まず、理解しないといけないことは
・
確率密度関数の確率密度(分布の縦軸)は、確率そのものではない
なぜか?
私「例えばt分布を使って、tがぴったり3になる確率を求めることはできないの?いつも、tが1より大きくて3より小さいみたいな「範囲」でしか議論できないの?」
→Copilot
目次
Copilot が送信しました:
良い質問です!確率密度関数(PDF)を使って、特定の値がぴったり出る確率を求めることはできません。これは、連続型の確率変数が無限に多くの値を取り得るためです。具体的な値が出る確率はゼロになります。
連続型の確率変数
連続型の確率変数(例えばt分布)は、無限に多くの値を取り得るため、特定の1つの値が出る確率はゼロです。したがって、tがぴったり3になる確率を求めることはできません。
範囲での確率
その代わりに、特定の範囲内に値が入る確率を求めます。例えば、tが1より大きくて3より小さい範囲の確率を求めることができます。このように範囲で議論することで、連続型の確率変数の確率を扱います。
例え話
例えば、サイコロを振るときに「3が出る確率」は1/6ですが、連続型の確率変数の場合は「3.000000…」と無限に続くため、特定の値が出る確率はゼロです。そのため、「3に非常に近い範囲」の確率を求めることになります。
t分布の例
t分布の場合、tが1より大きくて3より小さい範囲の確率を求めるには、累積分布関数(CDF)を使います。例えば、Pythonで計算する場合は次のようになります:Python
from scipy import stats
# 自由度を設定
df = 10
# tが1より大きくて3より小さい範囲の確率を計算
probability = stats.t.cdf(3, df) - stats.t.cdf(1, df)
print(probability)
AI で生成されたコード。ご確認のうえ、慎重にご使用ください。FAQ で詳細を確認。
このようにして、特定の範囲内に値が入る確率を求めます。
他に質問があれば、どうぞお知らせください!
・次。tがある値で出たとすると、それがどれくらいやばいのか?平均からどれくらい離れてるのか?を考えることになる。
t=3とでたら、それがどれくらいやばいのか?を知りたい。
じゃあ、3よりもひどい値になる確率ってこれくらいですよ
つまりt≧3となる確率は0.025ですよ、みたいなさ。そういう答え方をするわけよ。
ぴったり3になる確率っていうのは議論できないので。
(例え話)
りんごを八百屋で200個盗んだやつがどれくらいやばいか?
→今までに日本でりんごを200個以上盗んだ人は、戦後の歴史上に三人しかいません
→やばいやん!
ってなるのと同じ流れ。
・参考
私「高校までの確率の問題は、統計の分野を除けば、離散型の確率分布しか扱ってなかったんじゃないの?」→Copilot
Copilot が送信しました:
そうですね、高校までの確率の授業では、主に離散型の確率分布を扱うことが多いです。例えば、サイコロやコイン投げの問題などが典型的です。これらはすべて離散型の確率分布に基づいています。
離散型の確率分布
- サイコロ: 1から6までの目が出る確率はすべて1/6。
- コイン投げ: 表が出る確率と裏が出る確率はそれぞれ1/2。
- カード引き: トランプの特定のカードを引く確率など。
高校で扱う主な離散型の確率分布
- 二項分布: 成功か失敗かの2つの結果しかない試行を繰り返す場合の分布。
- 幾何分布: 初めて成功するまでの試行回数の分布。
- ポアソン分布: 一定の時間内に起こる事象の回数の分布。
連続型の確率分布
一方、連続型の確率分布は、大学レベルの統計学で本格的に学ぶことが多いです。連続型の確率分布には、正規分布やt分布などがあります。これらは、特定の範囲内での確率を求めるために使われます。
まとめ
高校までの確率の授業では、離散型の確率分布が中心ですが、統計学や大学レベルの数学では連続型の確率分布も重要な役割を果たします。これが、統計学が少し難しく感じられる理由の一つかもしれませんね。
・分布は研究され尽くされてる。
たとえばカイ二乗分布は、カイ二乗値がどのような値をとるかの分布。
カイ二乗値は基本正になる。
カイ二乗値は、表全体の値が、普通とどれくらい乖離してるか?を示すものなので。
カイ二乗分布は数学的背景ガチで難しい(笑)
でも何とか理解できるかも。
ガンマ関数(階乗の拡張版!)とか出てくる。
とりあえず、t値やカイ二乗値っていうのは、平均からどれくらいはなれてるかなーっていう数値
(カイ二乗値の平均は自由度。t値の平均は0です。)
平均というのも、足して数でわった→期待値→連続分布の真ん中 というように定義がどんどん進化してるんで。